HLJenga: Hexalink Jenga Manipulator

VIDEO DEMO

We were required to program QKM manipulators to play Jenga automatically
My part was doing hand-eye calibration, blob analysis, path/trajectory planning and simple UI
The robot operates like this:
1. Take a picture with camera and calculate target positions
2. Do path and trajectory planning
3. Upload planned trajectory to bot
4. Run

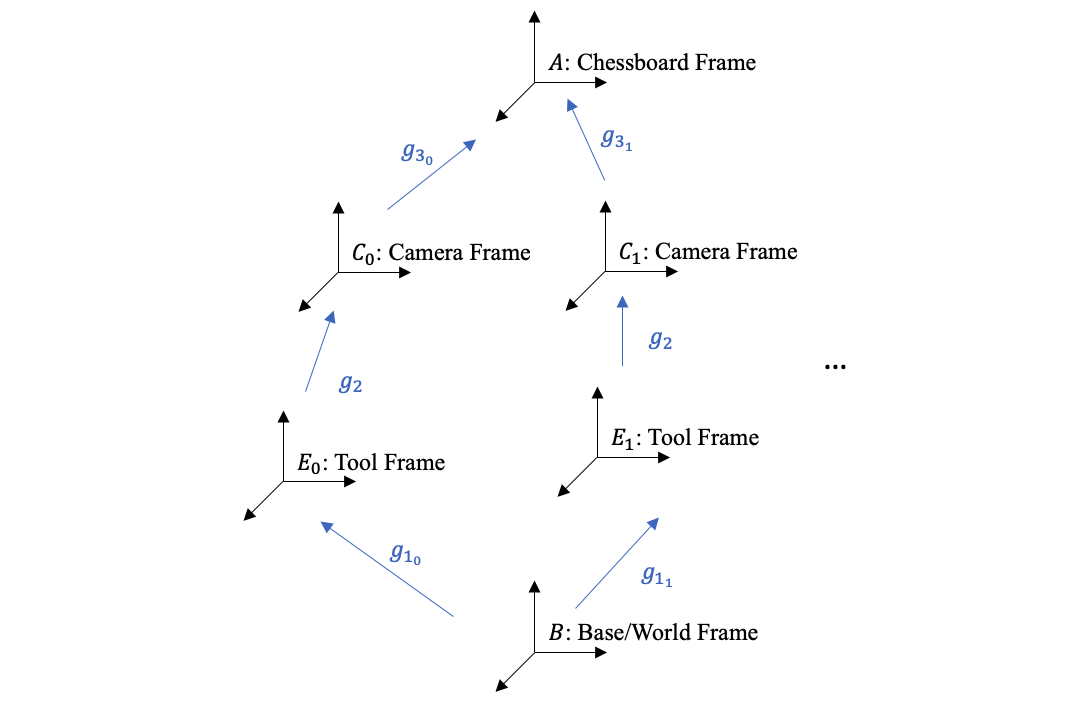
Aims to find the transform matrix from camera frame to tool frame.
Intrinsic params: cv::calibrateCamera()
Solve for pose of the calibration board in camera frame: cv::solvePnP()
Solve for end effector transformation matrix and use cv::calibrateHandEye() to finish the process

Consider the transformation $T_{E_1 \rightarrow C_0}=g_{1_1}^{-1}g_{1_0}g_2=g_2g_{3_1}g_{3_0}^{-1}$, where $g$ stands for the configuration of a frame
By taking N pictures, we can make use of N equations to solve $AX=XB$
Actual solver is implemented by OpenCV: cv::calibrateHandEye()
Subproblem 1: How to find $g_{3_i }$?
- cv::calibrateCamera()
- cv::solvePnP()
Subproblem 2: How to find $g_{1_i }$?
- Forward kinematics

Blob Analysis:
1. RGB to HSV
2. Get blob areas based on color filtering
3. Apply morphology process to eliminate cracks and dots
4. Find blob contours and corresponding minAreaRect
Coordinates transformation:
1. Pixel frame to camera frame: $q_{pixel}Z_c=KDq_{camera}$
2. Camera frame to world frame: $q_{world}=g_1g_2q_{camera}$
Sort targets by the distance to base in ascending order, because we need to take into consideration of the height of already built structure and make sure that the planned path does not crush it

Linear function with parabolic bends and via points Apply inverse kinematics with given starting, ending and via points to find corresponding points in joint space
Doing trajectory planning in joint space directly is much faster because of absence of calculating inverse
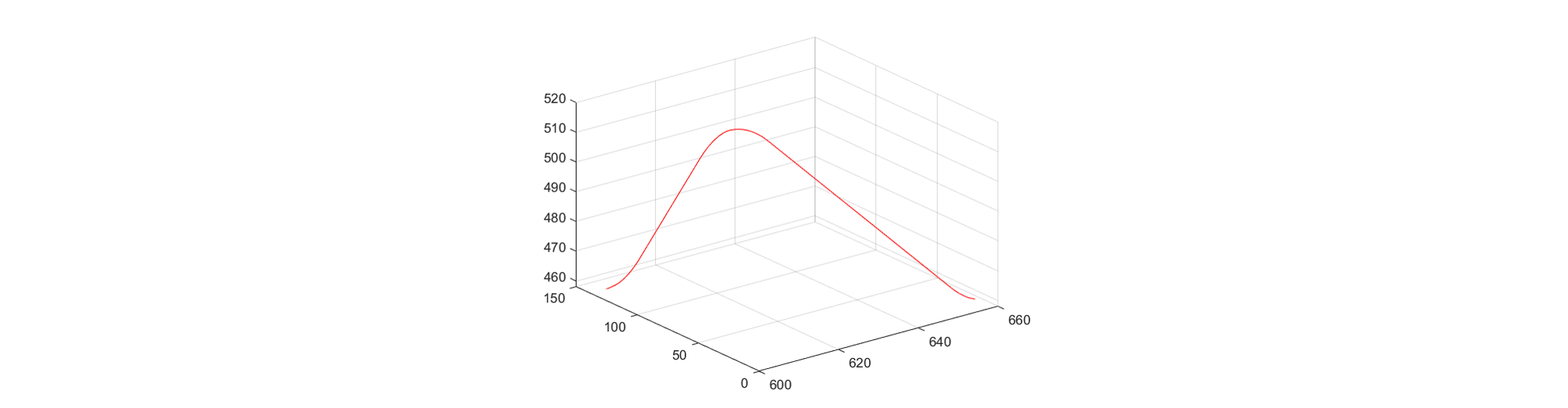
To avoid collision and damage, trajectories are first visualized in MATLAB